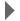The Hamiltonian describing the interaction between the spin operators of two nuclei can be written in the following form:
IA . J . IB
IA and IB are the spin operators of the two nuclei that are interacting and J is a tensor.
In solution, due to rapid averaging the contribution to the Hamiltonian from this interaction can be written as:
J IA . IB
Here, J, In solution NMR spectroscopy, J is a scalar and can be either positive, negative or zero. zero. If J is positive then, you have a positive coupling constant and if J is negative then you have a negative coupling constant.
Furthermore, if the coupling is weak (i.e., the chemical shift separation between the resonance frequencies of A and B is much greater than the magnitude of the coupling constant J), the contribution to the Hamiltonian from the J-coupling can be written as: J IAz . IBz
The theory of the physical mechanism of interaction between two spins spins, mediated through electrons (the J-coupling interaction) was described can be explained by Karplus.valence bond theory.
Essentially, the magnitude of the coupling constant depends upon the probability of electrons at the nucleus and the sign depends on the nature of the two nuclei that are coupled and the manner in which the interaction is mediated by the intervening electrons.
Regarding the second question. The resonance frequency is NOT changed by J-coupling (of alpha or of any other nuclear spin, whether 1J, 2J, ..). J-coupling is usually observable in the 1D-spectrum as a splitting of the resonance signal into a multiplet. multiplet.
Some relevant References:
Electron Coupled Interactions between Nuclear Spins in Molecules. Norman F. Ramsey. Phys. Rev. 91, 303–307 (1953).
Valence?Bond Interpretation of Electron?Coupled Nuclear Spin Interactions. Martin Karplus and D. H. Anderson. J. Chem. Phys. 30, 6 (1959)
Contact Electron?Spin Coupling of Nuclear Magnetic Moments. Martin Karplus. J. Chem. Phys. 30, 11 (1959)).
I believe the book by James Keeler would be a good introduction to the basic theory of NMR Hamiltonians, Spin Operators, etc.